최소 공통 조상(LCA, Lowest Common Ancestor)

Ancestor
Rooted Tree에서 root를 기준으로 높이가 정해집니다. root의 높이를 0이라고 둘 때 각각의 높이는 1씩 증가합니다.
이 때, 임의의 정점에서 '루트'로 향하는 최단경로에 존재하는 자신보다 height가 낮은 정점들을 Ancestor(조상) 이라고 합니다.
보통 바로 윗 조상을 Parent라고 부릅니다.
Common
주어진 두 임의의 정점은 각각 조상을 가집니다. [그림 1]에서 정점 a는 루트로 향하는 조상을 가지고, b도 가지고 있습니다.
이 때 두 정점의 조상들 중 공통된 조상을 공통 조상이라고 부릅니다.
[그림 1]에서는 보라색과 빨간색으로 칠해진 Common Ancestor가 있습니다.
Lowest
공통 조상들 중에서 깊이가 가장 낮은 조상을 LCA(Lowest Common Ancestor)라고 부릅니다.
LCA 알고리즘은 임의의 두 정점이 주어질 때, 이들의 최소 공통 조상을 찾기 위한 알고리즘입니다.
그렇다면 공통된 조상들을 찾기 위해 어떻게 접근하면 될까요..
단순하게 생각해보기
- 최소 공통 조상을 찾기 위해서 가장 쉽게 접근해본다면 주어진 정점들에서 root로 가는 모든 경로의 조상을 찾고, 각각의 경로에서 처음으로 겹치는 조상을 찾으면 될 것 같습니다.
- 그런데, 이 때 비교를 하려면 높이를 통해서 더 낮은 깊이의 조상을 먼저 움직이게 되기 때문에, 이를 고려하여 생각한다면 다음과 같습니다.
- 높이를 맞춘다.
- 높이가 맞춰졌으니 순차적으로 같이 높이를 올려가며 조상을 찾아본다.
https://www.acmicpc.net/problem/11437
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static int[] parent;
static int[] depth;
static boolean[] visited;
static ArrayList<Integer>[] tree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
tree = new ArrayList[N + 1];
visited = new boolean[N+1];
depth = new int[N+1];
parent = new int[N+1];
for (int i = 0; i < N + 1; i++) tree[i] = new ArrayList<>();
for(int i =0;i<N-1;i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
tree[u].add(v);
tree[v].add(u);
}
// parent배열과 depth배열을 초기화할 수 있습니다.
dfs(1,0);
int M = Integer.parseInt(br.readLine());
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
sb.append(LCA(u, v)).append('\n');
}
System.out.println(sb);
}
public static void dfs(int num, int height){
visited[num] = true;
depth[num] = height;
for(int next : tree[num]){
if(!visited[next]){
parent[next] = num;
dfs(next, height+1);
}
}
}
public static int LCA(int u, int v){
//항상 한쪽(v)를 더 낮은 위치에 두기 위해 SWAP합니다.
if(depth[u] > depth[v]){
int tmp = u;
u = v;
v = tmp;
}
//높이 맞추기
while(depth[v] != depth[u]){
v = parent[v];
}
if(u == v) return u;
//같은 높이이므로 하나씩 같이 올려서 확인한다.
while(u != v){
u = parent[u];
v = parent[v];
}
return u;
}
}
이와 같은 방식으로 접근했을 때, worst한 case에는 O(N)의 시간 복잡도를 가지게 됩니다.
루트를 기준으로 'ㅅ'자 모양으로 퍼진 마지막 leaf Node두개를 잡을 때 가장 worst한 case가 됩니다.
LCA의 목표는 단순히 두 정점 사이의 공통 조상을 찾는 것도 있지만, 그러한 질의들이 무수하게 요청될 때 빠르게 찾아내는데 있습니다.
질의 M개에 대해 위와 같은 방식으로 응답하게 되면 O(NM)이라는 시간이 걸리게 됩니다.
query에 빠르게 응답하기 위해서는 먼저 계산된 어떠한 값들을 전처리해 두고, 응답을 해줍니다.
우리는 빠르게 응답하기 위해 O(NlogN)의 전처리 과정을 거쳐 O(logN)에 질의에 응답해보고자 합니다.
한 번 더 생각해보기
단순하게 생각했을 때 가장 크게 문제가 되는 점은, 깊이가 깊어질 수록, 한칸씩 모두 봐야한다는 점이였습니다.
(worst case에서 볼 수 있듯이 그렇습니다)
이러한 문제점을 해결하기 위해 크게 크게 뛰어 보자 라는 생각을 가지고 접근하게 됩니다.
우선 다르게 생각해보기 전에 다음을 생각해봅시다.
수직선 상에서 어떠한 임의의 점을 찾아간다고 해봅시다.
이 때 우리는 어떠한 수직선 상으로 ‘이동’할 수 있고 이 때마다 찾고자 하는 임의의 점보다 크다, 아니다(true, false)를 가르쳐 준다고 했을 때, 빠르게 찾을 수 있는 방법은 다음과 같습니다.

1. 처음에 뛸 수 있는 가장 큰 수 만큼 뛰어봅니다.
2. 이 때 임의의 점 보다 크다고 하니 더 반틈 작게하여 뛰어봅니다.
뛰어보니, 임의의 점보다 작다고 합니다. 그렇다면 우리가 처음에 뛰었던 가장 큰수 (2K) 그리고 다음에 뛴 수 (2K−1) 안에 우리가 찾고자 하는 점이 있겠군요.
그럼 우리는 다시 2K−1로 이동하여 반복해서 찾아봅시다.
이때, 임의의 점이 있을 범위가 2K−1이므로 2K−1만큼 뛰는 것이 아닌 또 반틈을 줄여
2K−2를 뛰어봅니다. 이를 반복하게 되면 결국 찾게 되겟죠.
LCA를 빠르게 찾아가는 과정 또한 이와 비슷한 생각에서 출발합니다.
우리가 해결하고자 하는 문제점이였던 ‘크게 크게 뛰어 찾아보자’라는 문제와 동일하다는 의미이죠.
높이가 같은 각 점에서 2K 위의 조상만큼 뛰어 확인해보았을 때, 만약 조상이 같다면, [그림 1]에서 빨간 점일 수 있다고 생각하고 더 밑일 수도 있겠다 생각하고 범위를 좁혀나가는 겁니다.
"공통 조상일 수도 있겠구나"라고 하는 말은 결국 [그림2]에서 너무 멀리 뛰어서 우리가 찾으려는 점은 더 왼쪽에 더 밑에 있을 수도 있겠구나라고 생각하는 것과 같습니다.
자, 우리는 이제 어떻게 하면 "빠르게 뛰어서 찾아 나가지?"하는 LCA의 아이디어를 알게 되었습니다.
이 아이디어를 구현하기 위해 우리에게 필요한 것은 어떠한 노드 X에서의 2K떨어진 조상은 어디 있는가 입니다.
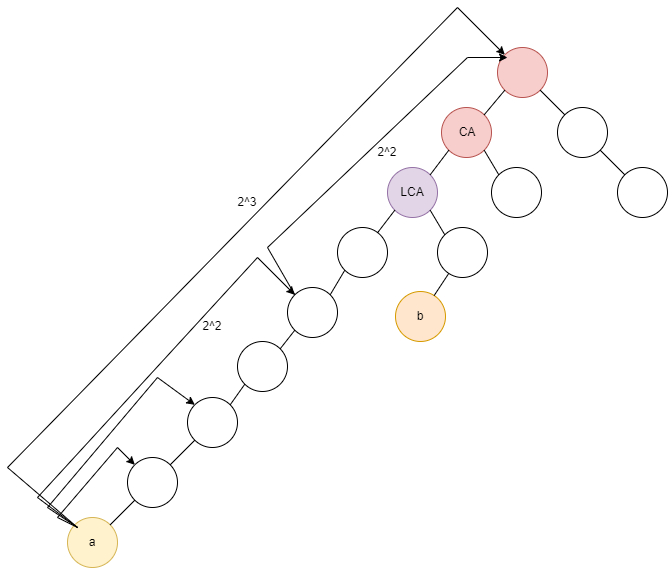
우리가 궁금한 2K떨어진 곳을 찾아봅시다.
[그림 3]을 보게 되면 나와 어떠한 조상간의 거리는 2K가 됩니다. 이 때, 만약 우리가 2K−1을 알고 있다면,
'나의 2K−1조상의 2K−1 조상이 나의 2K 조상' 이됩니다.
말이 어려워서 그렇지 사실 거리 2K = 2K−1 + 2K−1이라 두번 가는 것과 마찬가지 입니다.
우리는 여기서 점화식을 세울 수 있습니다.
parent[현재 나의 노드][X] = 현재 나의 노드로 부터 2X번째 조상을 의미한다고 한다면,
parent[curNode][K] = parent[ parent[curNode][K-1] ] [K-1]
즉, 결국 우리가 구하기 위해 필요한 조상의 정보는 위의 점화식을 활용하여 dp로 풀어낼 수 있습니다.
정리해보자
정리하자면,
1. 단순하게 생각했을 때 높이를 같게하고 하나하나씩 올라가며 LCA를 찾아보자
2. 근데, 어떠한 값을 찾아 올라가는데 시간이 너무 많이 걸린다.
2. 2의 제곱 수 만큼 빠르게 올라가보자.
3. 그러한 조상노드가 어딘지 알아야 갈 수 있으니, 이를 찾아보자
https://www.acmicpc.net/problem/11438
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static int N,K;
static ArrayList<Integer>[] tree;
static int[] depth;
static int[][] parent;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
tree = new ArrayList[N+1];
//find Height
K = findHeight(N);
//cache hit 생각하면 반대로가 낫다고 함.
parent = new int[N+1][K];
depth = new int[N+1];
visited = new boolean[N+1];
for(int i =0;i<N+1;i++){
tree[i] = new ArrayList<>();
}
StringTokenizer st;
for(int i =0;i<N-1;i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
tree[u].add(v);
tree[v].add(u);
}
//preProcessing LCA
preprocessLCA();
int M = Integer.parseInt(br.readLine());
for(int i =0;i<M;i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
sb.append(LCA(u, v)).append('\n');
}
System.out.println(sb);
}
//전처리
public static void preprocessLCA(){
dfs(1,0);
//2^K 조상 찾기
for(int i = 1;i<K;i++){
for(int cur=1;cur<N+1;cur++){
//내 2^j번째 부모는 나의 2^j-1한번째 부모의 j-1한번째 부모.
parent[cur][i] = parent[parent[cur][i-1]][i-1];
}
}
}
public static void dfs(int num, int height){
visited[num] = true;
depth[num] = height;
for(int next : tree[num]){
if(visited[next]) continue;
parent[next][0] = num;
/* for(int i =1;i<K;i++){
if(parent[next][i-1] ==0) break;
parent[next][i] = parent[parent[next][i-1]][i-1];
}*/
dfs(next,height+1);
}
}
public static int LCA(int u, int v){
//항상 u가 위쪽에 있도록.
//그니까 depth[u]가 항상 작도록.
if(depth[u] > depth[v]){
int tmp = u;
u = v;
v = tmp;
}
//높이 맞춰주기
// 이 때도 그냥 하나씩 올리기보다는
// 구해놓은 값을 활용하여 2의 제곱 수로 올라갑니다.
// ex) 두 노드 깊이 차이가 13이라면
// 13 = 1101(2) 이기 때문에 각 자리 수만큼 조상으로 올라가면 됩니다.
for(int i=K-1;i>=0;i--){
if((depth[v]-depth[u] & 1<<i) > 0){
v = parent[v][i];
}
}
//같다면
if(u == v) return u;
//같은 위치 맞추었고 올라가보자.
//우리가 생각한 아이디어대로 구현
for(int i = K-1;i>=0;i--){
if(parent[u][i] != parent[v][i]){
u = parent[u][i];
v = parent[v][i];
}
}
return parent[u][0];
}
private static int findHeight(int N) {
int tmp = N;
int K = 0;
while (tmp > 0) {
K++;
tmp /= 2;
}
return K;
}
}
시간복잡도
각 노드들에 대해 logN만큼의 조상들을 구하게 되므로 전처리 과정은 O(NlogN)이됩니다.
이후 질의를 처리하는 과정은 O(logN)이 됩니다.
활용
lca는 두 정점 사이의 공통 조상을 찾는 데 이용됩니다.
다르게 생각해본다면, 두 정점이 위로 올라가면서 만나는 첫번째 지점으로 이 때,
두 정점은 이어지게 됩니다. 즉, LCA를 활용하면 두 정점의 거리를 계산할 수 있습니다.
추천 문제
위에서 링크를 단 LCA 문제들을 제외하고
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV5LnipaDvwDFAXc
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
풀어볼 문제들
15480번: LCA와 쿼리 (★)
1761번: 정점들의 거리
8012번: Byteasar the Travelling Salesman
1396번: 크루스칼의 공 (★)
이후 추천할 문제가 생기면 추천해보도록 하겠습니다.
조금 더 LCA에 대한 이해를 원하신다면 신찬수 교수님의 Search in the dark Series(3편)을 보시는 걸 추천합니다.
'알고리즘 > 이론 및 스킬' 카테고리의 다른 글
| Parametric Search (0) | 2022.02.09 |
|---|---|
| 소팅 (0) | 2022.02.07 |
