[SWEA] 그래도 수명이 절반이 되어서는...

문제 링크 

SW Expert Academy

1. 문제의 유형 및 이해

이분탐색(parametric Search) 

 

N개의 블록으로 구성된 플래쉬 드라이브에서 주어지는 덩어리 순서대로 덩어리를 구성하고자 한다.

“그래도 수명이 절반이 되어서는” 안된다는 정책에 따라서 초기 데이터를 플래시 드라이브의 적절한 위치에 배치하여 드라이브 수명을 최대한 길게 하고 싶다.

위의 예는 플래시 드라이브 블록들의 Wear Level을 표시한 것이다.

초기 데이터가 3개의 덩어리로 구성되어 있고 각 덩어리의 블록 수가 2, 1, 3이라고 하면 다음과 같이 저장했을 때 최대 Wear Level이 3이 되어 최적이 된다.

입력으로 플래시 메모리의 블록 수 N, 각 블록의 Wear Level 값, 초기 데이터의 덩어리 수와 각덩어리가 차지하는 블록 수를 받아서 위의 조건을 만족하도록 저장할 때

가능한 최대 Wear Level의 최소값을 구하는 프로그램을 작성하라.

 

우리가 구하고자 하는 건 "가능한 최대 Wear Level"의 해 중 "최소 값"을 구하는 문제입니다.

parametric search를 모르신다면 위의 링크를 참조하셔도 좋을 것 같습니다.

 

데이터의 덩어리수가 200,000 만개로 모든 case를 찾아 구하기에는 범위가 매우 큽니다.

이 때 우리가 구하고자 하는 최적화 문제를 결정 문제로 변환하여 parametric search 를 통해 진행합니다.

2. 문제 접근 방법

구하고자 하는 최적화 문제는 "가능한 최대 Wear Level"의 해 중 최소 값을 구하는 문제입니다.

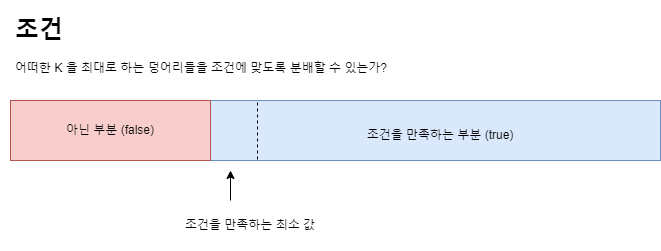
이 문제를 결정 문제로 변환시켜보면 "어떤 WearLevel K가 주어질 때 조건을 만족할 수 있을까?"가 됩니다.

조건을 만족하는 모든 해 중에서 가장 작은 해를 찾아보도록 합니다.

 

해당 문제를 parametric search로 풀 수 있는 이유는 구하고자 하는 WearLevel에 따라 답이 연속적으로 sequential하게 존재하기 때문입니다.

 

"가능한" 에 집중해보도록 합시다.

문제에서 조건에 가능하다는 의미는 "어떤 최대 level보다 낮은 값들이 있는 사용 가능한 영역에서 덩어리를 구성할 수 있다"는 뜻입니다.

즉, WearLevel이 낮을 수록 덩어리를 구성할 수 있는 영역이 좁아지고  

WearLevel을 배열에서 가장 큰 값으로 설정한다면, 모든 데이터 영역을 사용할 수 있게 됩니다.

 

그러면 우리는 만들 수 있는 덩어리들의 배열을 이용하여 문제에서 요구한 덩어리를 만족 시킬 수 있도록 분할하였을 때, 분할이 "가능하다" 와 "가능하지 않다"로 나눌 수 있게 됩니다.

 

즉, WearLevel 값에 따라서 낮을 수록 사용할 수 있는 메모리가 적고, 클수록 많아져서 연속적으로 값이 분포하게 됩니다.

 

구현은 다음과 같습니다. 

 - 어떤 WearLevel로 만들 수 있는 덩어리의 크기들을 찾아본다.

 - 만들수 있는 덩어리 크기에서 차례대로 내가 만들려는 덩어리 크기만큼 빼 본다.

 - 만약에 내가 만들려는 덩어리 크기를 다 뺀다면, 즉 구성할 수 있다면 True

 - 아니라면 False

    import java.io.BufferedReader;
    import java.io.IOException;
    import java.io.InputStreamReader;
    import java.util.ArrayList;
    import java.util.Arrays;
    import java.util.StringTokenizer;

    public class Solution {
        static int[] data;
        static int[] group;
        static int max;
        static int N,K;
        public static void main(String[] args) throws IOException {
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
            StringBuilder sb = new StringBuilder();
            StringTokenizer st;
            int T = Integer.parseInt(br.readLine());
            for (int test_case = 1; test_case <= T; test_case++) {
                sb.append('#').append(test_case).append(' ');
                st = new StringTokenizer(br.readLine());
                N = Integer.parseInt(st.nextToken());
                K = Integer.parseInt(st.nextToken());
                data = new int[N];
                st = new StringTokenizer(br.readLine());
                max = -1;
                for(int i =0;i<N;i++){
                    data[i] = Integer.parseInt(st.nextToken());
                    max = Math.max(max, data[i]);
                }
                group = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
                sb.append(findByBinarySearch()).append('\n');
            }
            System.out.print(sb);
        }
        public static int findByBinarySearch(){
            int left =0;
            int right = max;
            int pos = -1;
            int mid;
            while(left<=right){
                mid = (left+right)>>1;
                /--------------- 결정을 위해 조건을 만족시키는지 값을 찾음. -------------/
                int[] cnt = countBlock(mid);
                int groupPointer =0;
                for(int i =0;i<cnt.length;i++){
                    while(groupPointer <group.length){
                        if(cnt[i] < group[groupPointer]) break;
                        cnt[i] -= group[groupPointer++];
                    }
                }
                /------------------------------------------------------------/
                
                //조건이 만족하는가?
                //true라면 더 낮은 값도 확인해보자.
                if(groupPointer == group.length){
                    pos = mid;
                    right = mid -1;
                }else{
                    left = mid +1;
                }
            }
            return pos;

        }
        
        //최대 WearLevel 크기가 maxLevel일 때 구성할 수 있는
        //덩어리 영역
        public static int[] countBlock(int maxLevel){
            ArrayList<Integer> blocks = new ArrayList<>();
            int idx =0;

            while (idx != N) {
                if (data[idx] > maxLevel) {
                    idx++;
                    continue;
                }
                int cnt = 0;
                while (data[idx] <= maxLevel) {
                    cnt++;
                    idx++;
                    if (idx == N) break;
                }
                blocks.add(cnt);

            }
            int[] ret = new int[blocks.size()];
            for(int i =0;i<ret.length;i++){
                ret[i] = blocks.get(i);
            }
            return ret;
        }
    }